#1956. 운동

📖Problems

V개의 마을와 E개의 도로로 구성되어 있는 도시가 있다. 도로는 마을과 마을 사이에 놓여 있으며, 일방 통행 도로이다. 마을에는 편의상 1번부터 V번까지 번호가 매겨져 있다고 하자.

당신은 도로를 따라 운동을 하기 위한 경로를 찾으려고 한다. 운동을 한 후에는 다시 시작점으로 돌아오는 것이 좋기 때문에, 우리는 사이클을 찾기를 원한다. 단, 당신은 운동을 매우 귀찮아하므로, 사이클을 이루는 도로의 길이의 합이 최소가 되도록 찾으려고 한다.

도로의 정보가 주어졌을 때, 도로의 길이의 합이 가장 작은 사이클을 찾는 프로그램을 작성하시오. 두 마을을 왕복하는 경우도 사이클에 포함됨에 주의한다.

입력

첫째 줄에 V와 E가 빈칸을 사이에 두고 주어진다. (2 ≤ V ≤ 400, 0 ≤ E ≤ V(V-1)) 다음 E개의 줄에는 각각 세 개의 정수 a, b, c가 주어진다. a번 마을에서 b번 마을로 가는 거리가 c인 도로가 있다는 의미이다. (a → b임에 주의) 거리는 10,000 이하의 자연수이다. (a, b) 쌍이 같은 도로가 여러 번 주어지지 않는다.

출력

첫째 줄에 최소 사이클의 도로 길이의 합을 출력한다. 운동 경로를 찾는 것이 불가능한 경우에는 -1을 출력한다.

예제 입력 1

예제 출력 1

3

🔍Institution

키워드 : 일방통행 도로, 사이클 찾기, 도로 길이의 합이 최소

V : 마을, E : 도로

🔍Approach

1. 일단 하기

딕셔너리 생성 { i : }
입력받은 값들을 오름차순으로 정렬한다.
시작노드를 설정한 후 사이클이 생성되는지 확인
- 생성되지 않다면 방문했다는 것을 seen[]에 추가하고 다음 노드로 넘어감
- 생성되었다면 seen[]에 추가하고 거리를 dis[]에 저장함
- 위 과정을 반복함
사이클이 생성되지 않았다면 break를 하고 -1 return
min()을 이용해서 dis[]에 최솟값을 구함

→ 모르겠음…

2. 최소 경로 문제 푸는 법 이용하기

최단 경로 탐색 알고리즘(DP)

다익스트라 알고리즘 : ‘하나의’ 정점에 출발했을 때 다른 모든 정점으로의 최단 경로 구하는 알고리즘
플로이드 와샬 알고리즘 : ‘모든 정점’에서 ‘모든 정점’으로 최단 경로를 구하는 알고리즘
⇒ 시작점을 지정해주지 않았기 때문에 플로이드 와샬 알고리즘 사용하기

플로이드 와샬 알고리즘

플로이드 와샬은 다익스트라 알고리즘과 같이 최단거리 혹은 최소비용을 구하는 알고리즘
다익스트라 알고리즘과는 달리 모든 노드에서 다른 모든 노드들까지의 최소 거리(혹은 최소비용)을 구하기 때문에 “어딘가를 경유한다.”라는 조건이 주어질 때, 사용을 고려하기 좋은 알고리즘
다만, 출발점(s), 도착지점(e), 경유지(p)에 모든 노드를 고려해야하므로 시간 복잡도는 O(N^3)으로 큰 편
즉, 문제에서 주어진 노드(N)의 최댓값을 고려해 미리 계산해 사용할 가치가 있는 알고리즘인지 고려해야 함

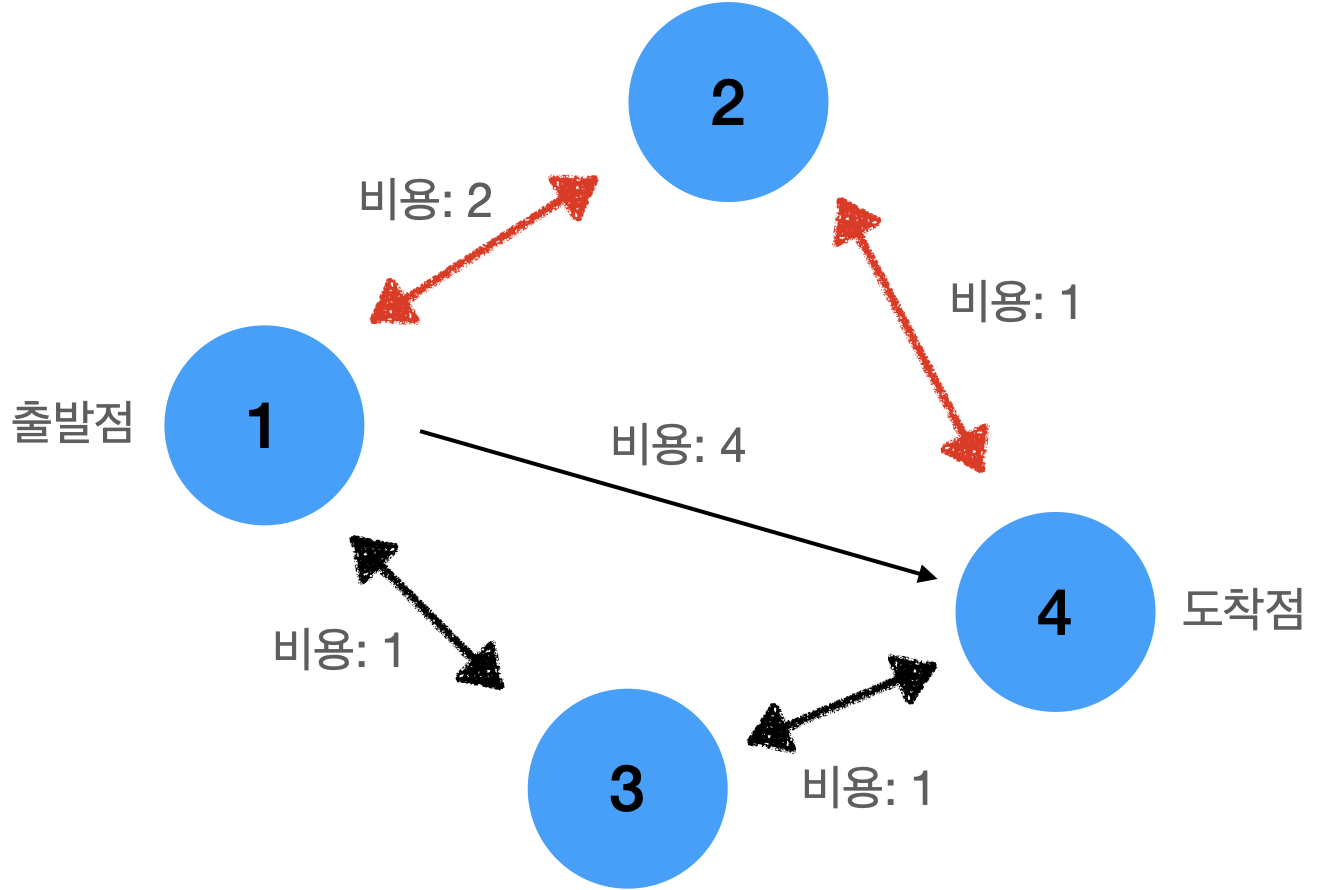
위 그림의 경우는 출발지점이 1번 노드, 도착지점이 4번 노드인 경우

1 → 4로 가는게 경유지 없이 간다면 비용은 4가 들게된다.

만약 경유지를 선택하게 될 때, 2번을 경유지로 선택한다면 총 비용은 3(2 + 1)이고 3을 경유지로 선택한다면 비용은 2(1 + 1)이 된다.

따라서 위 그림의 최소 비용(혹은 최단 거리)는 1 -> 3 -> 4를 선택한 2가 된다.

이제부터 1 -> 4로 이동할 때 발생하는 최소비용은 2라는 것을 알 수 있다.

플로이드 와샬은 이처럼 모든 노드를 방문해서 다른 노드까지의 최소비용을 계속 갱신해주면서 모든 노드에서 모든 노드까지(몇 번을 경우하는지 상관없이) 최소 비용을 알아낼 수 있다.

출처 : https://reinvestment.tistory.com/72

✏️ 플로이드 와샬 알고리즘 코드(파이썬)

  
cost = [[INF] * n for _ in range(n)]# INF로 구성된 n x n 행렬, 노드끼리의 최소 비용을 담을 배열for i in range(n):# 자기자신 -> 자기자신의 비용은 0이므로 초기화 해준다.
	cost[i][i] = 0

# 플로이드 와샬for k in range(n):# 경유지for j in range(n):# 도착지for i in range(n):# 출발지# 현재 i -> j까지드는 비용이 i -> k -> j의 비용보다 비싸다면 더 저렴한 비용으로 갱신if cost[i][j] > cost[i][k] + cost[k][j]:
                    cost[i][j] = cost[i][k] + cost[k][j]

여기서 INF는 중간 값으로 주어진 나올 수 있는 값보다 큰 값으로 세팅한다.
cost 배열은 출발지점 → 도착지점 까지의 비용을 담아 놓을 2차원 배열이다.
출발점, 도착점, 경유지를 모두 탐색하는 3차원 for문을 돌면서 현재의 비용(i → j)보다 k를 경유하는 (i -> k -> j) 비용이 더 저렴하다면 갱신해 주면 플로이드 와샬 구현이 완료됨
- 이때, 경유지를 기준으로 모든 경우(출발, 도착)을 확인해야하므로 최상단 for문에는 경유지(k)가 와야한다.
- 그렇지 않을 경우, 모든 경우에서 제대로 갱신되지 않을 수 있다.

문제 분석

경유지 출발지 도착지 → for문

i \ j	1번 마을	2번 마을	3번 마을
1번 마을	0	1	5
2번 마을	INF	0	2
3번 마을	INF	1	0

i : 출발지, j ; 도착지, k : 경유지

🚩My submission

pypy3로 제출해야 함 python3로 제출하면 시간초과 뜸

pw로 설정한 테이블을 infinity로 초기화한다. 이곳에 마을의 거리를 저장한다. min_dist는 최단 거리를 구해야 하므로 infinity로 초기화한다.
만든 테이블 pw에 x, y, dist(거리)를 입력받은 후, x, y가 해당하는 인덱스에 거리를 저장한다.
플로이드 와샬 알고리즘
- i는 출발지, j는 도착지, k는 경유지이며 3중 for문을 돌면서 비교한다. 출발지-경유지, 경유지-도착지를 더한 값 (pw[i][k] + pw[k][j])이 원래 출발지-도착지(pw[i][j])에 해당하는 값보다 작다면 출발지-도착지 값을 바꿔준다.
- 이때, 경유지를 기준으로 모든 경우(출발, 도착)을 확이해야하므로 최상단 for문에는 경유지(k)가 와야한다. 그렇지 않을 경우, 모든 경우에서 제대로 갱신되지 않을 수 있다.
answer와 pw[i][i]에 해당하는 값 중 더 작은 값을 min_dist에 넣어준다.
경로가 아예 없을 수도 있으므로, answer가 infinity라면 -1을 출력하고 그게 아니라면 min_dist를 출력한다.

  
V, E =  map( int, input().split()))
pw = [[[INF] * V ] * V]
min_dist = INF

# 마을과 거리를 입력 
for i in range(V+1):
    x, y, dist = map( int, input().split()))
    pw[x][y] = dist

# i : 출발지, j : 도착지, k : 경유지
for k in range(1,V+1):
    for i in range(1, V+1):
        for j in range(1, V+1):
            # 안 클 경우 저장
            if pw[i][k] + pw[k][j] < pw[i][j]:
                pw[i][j] = pw[i][k] + pw[k][j]
            else:
                continue
answer = inf
for i in range(V+1):
    min_dist = min(answer, pw[i][i])   

if min_dist == INF:
    print(-1)
else:
    print(min_dist)

🚩Others submission

다익스트라 알고리즘을 이용한 풀이 (python3로 제출해도 시간초과가 뜨지 않음)

  
import sys
import heapq

# 전처리 부분
input = sys.stdin.readline
INF = sys.maxsize

# 알고리즘 부분
def dijkstra():
    while heap:
        distance, start, end = heapq.heappop(heap)

        # 출발점과 도착점이 같다면 사이클이며, 힙에서 뽑은 경로이기 때문에 해당 값이 최소 경로가 됨
        if start == end:
            print(distance)
            break

        if dist[start][end] < distance: continue

        for n_dist, n_node in graph[end]:
            if dist[start][n_node] > distance + n_dist:
                dist[start][n_node] = distance + n_dist
                heapq.heappush(heap, [dist[start][n_node], start, n_node])

# 변수 선언 및 초기화 부분
v, e = map(int, input().split())
graph = [[] for _ in range(v + 1)]
dist = [[INF] * (v + 1) for _ in range(v + 1)]
heap = []

# 메인 코드 부분
for _ in range(e):
    a, b, c = map(int, input().split())
    graph[a].append([c, b])
    heapq.heappush(heap, [c, a, b]) # 유효한 경로를 미리 힙에 저장

dijkstra()다시 돌아오는 사ㅣ

단방향 그래프에서 시작점에서부터 이동하여 다시 돌아오는 사이클 중 최단 경로를 구하는 문제로 다익스트라 알고리즘을 사용하여 구현할 수 있다.

플로이드 와샬을 이용한 풀이

  
import sys
V, E = map(int, input().split())
INF = 10000 * V + 1 #전체 사이클을 돌 경우 최댓값 +1
distance = [[INF for _ in range(V+1)] for _ in range(V+1)]

for _ in range(E):
    start, end, dist = map(int, sys.stdin.readline().split())
    distance[start][end] = dist

#플로이드 워셜 알고리즘
for k in range(1, V+1):
    for i in range(1, V+1):
        for j in range(1, V+1):
            distance[i][j] = min(distance[i][j],
                                 distance[i][k] + distance[k][j])

#가장 작은 사이클 찾는 for문
min_cycle = INF
for i in range(1, V+1):
    min_cycle = min(min_cycle, distance[i][i])
    
if min_cycle == 10000 * V + 1: #사이클이 없을 경우
    print(-1)
else:
    print(min_cycle)

💡Retrospect

이런 유형은 정말 싫다. 그래서 스터디에서 문제 풀 때 하기 싫은 마음이 튀어나와서 더 내가 잘 못 풀게 했던 것 같다. 이런 문제가 내 약점인건데 자꾸 피하고 하기 싫어하지 말고, “오히려 좋아!!!” 생각하면서 문제를 마주보려고 노력해야겠다.
(은지가 내 멱살을 잡고 끌어줬다.. 고마워)
새롭게 알게 된 것 : 플로이드 와샬 알고리즘, 다익스트라 알고리즘
- 2가지 모두 단반향 그래프에 대해 다시 돌아오는 사이클 중 최단 경로를 구할 때 사용하는 알고리즘이다.
- 다익스트라 알고리즘 : ‘하나의’ 정점에 출발했을 때 다른 모든 정점으로의 최단 경로 구하는 알고리즘
- 플로이드 와샬 알고리즘 : ‘모든 정점’에서 ‘모든 정점’으로 최단 경로를 구하는 알고리즘
  - 출발지, 경유지, 도착지를 3중 for문을 이용해 탐색한다.

백준 - 1956. 운동 (MJ)